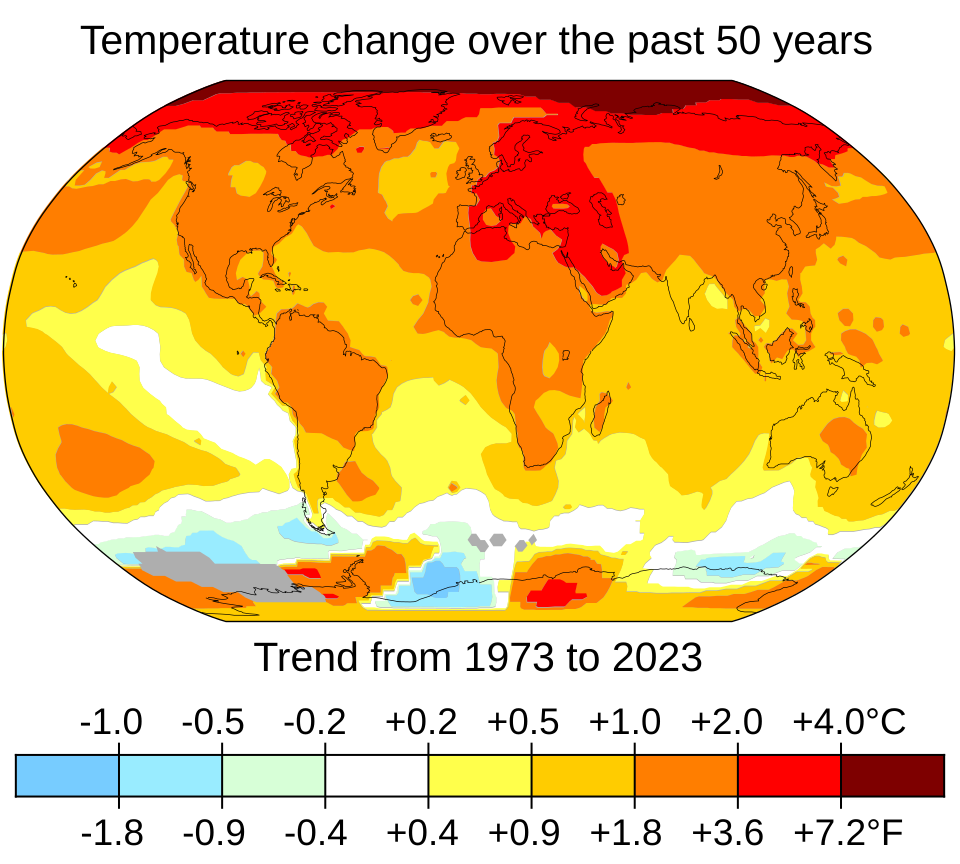
Das Trump-Lager hat letztes Jahr im Wahlkampf behauptet, die Demokraten hätten einen Hurrikan erzeugt und auf republikanisch regierte Bundesstaaten umgelenkt. Und Trump hat auch schon mal die Vorhersage für die Zugbahn eines Hurrikans geändert. Das ist so, als würde Frau Weidel sagen, die Vorhersage des Deutschen Wetterdienstes stimmt nicht und in Wirklichkeit wird der Sturm dahinziehen. Das ist völlig irre. (Jochem Marotzke, Direktor am Max-Planck-Institut für Meteorologie, 14. März 2025 )
Beginn der Wetterforschung
Während ein Verfahren zur numerischen Lösung gewöhnlicher Differentialgleichungen schon von Leonhard Euler in seinem 1768 erschienenen Buch “Institutiones Calculi Integralis” vorgestellt wurde, begann die numerische Behandlung partieller Differentialgleichungen erst im 20. Jahrhundert.
Der Meteorologe Lewis Richardson schlug in seinem 1922 erschienen Buch “Weather Prediction by Numerical Process” (das in seinem ersten, 1916 vollendeten Entwurf noch “Weather Prediction by Arithmetical Finite Differences” geheißen hatte) eine numerische Wettervorhersage vor. 64000 (menschliche) Rechner sollten ausreichen, das weltweite Wetter schnell genug für eine tägliche Meldung zu berechnen. Für seine numerische Wettervorhersage überzog er die Weltkarte mit einem Schachbrettmuster, wobei die Felder eine Seitenlänge von etwa 200 Kilometer hatten. Die Atmosphäre oberhalb jedes dieser Felder unterteilte er weiter in Schichten mit Grenzen in 2000, 4200, 7200 und 11800 Metern Höhe. Beinahe die Hälfte seines Buches bestand dann aus einer Diskussion der notwendigen physikalischen Gleichungen, um möglichst alle physikalischen Vorgänge, die sich zwischen diesen Zellen abspielen, zu berücksichtigen.

Wettervorhersagen gab es auch vorher schon, sie beruhten aber auf den Erfahrungen der Meteorologen und nicht auf den Differentialgleichungen der Physik. Tatsächlich galt auch Richardson Methode zum Zeitpunkt ihres Erscheinens als unpraktikabel und spielte in Lehrbüchern der Meteorologie keine Rolle bis Jahrzehnte später (maschinelle) Rechner gebaut werden konnten.
Anfänge der Numerik
In Deutschland hatte Felix Klein um die Jahrhundertwende – beeindruckt von Maschinenlaboratorien, die er auf seiner ersten USA-Reise besichtigt hatte – bei Industriellen für privat mitfinanzierte Universitätslaboratorien geworben, was letztlich zur Gründung der Göttinger Vereinigung zur Förderung der angewandten Physik und Mathematik führte. Als Begründer der numerischen Mathematik galt dann Carl Runge, dem man die Etablierung numerischer Rechen- und Approximationsverfahren (und ihrer praktischen Durchführung mit Rechenmaschinen) als eigene Disziplin der Mathematik verdankt.
Die effektive Bestimmung von Näherungslösungen ist natürlich schon seit dem Altertum – damals vor allem in China und Indien – ein Thema der Mathematik. Bis ins 19. Jahrhundert entstanden numerische Methoden aber stets im Kontext technischer oder naturwissenschaftlicher Anwendungen und stellten kein eigenständiges Gebiet der Mathematik dar. Neben dem Gaußschen Eliminationsverfahren und dem Gauß-Jordan-Algorithmus zur Lösung linearer Gleichungssysteme wurden etwa zur Lösung gewöhnlicher Differentialgleichungen das Runge-Kutta-Verfahren (Einschrittverfahren) und das Adams-Moulton-Verfahren (Mehrschrittverfahren), und zur Lösung partieller Differentialgleichungen beispielsweise die 1908 veröffentlichte Rayleigh-Ritz-Methode, die man als Vorgänger der Finite-Elemente-Methode sehen kann, entwickelt. Auch diese Verfahren entstanden jeweils im Zusammenhang mit konkreten Anwendungsgebieten, das Runge-Kutta-Verfahren etwa in der Aerodynamik. Berechnungen wurden in dieser Zeit noch mit einfachen Geräten oder von Hand durchgeführt.
Arbeiten, die man heute der numerischen Mathematik zurechnen würde, waren aber oft eher innermathematisch motiviert, etwa um ein besseres Verständnis von Differentialgleichungen zu erreichen. Zum Beispiel wurden Finite-Differenzen-Methoden in der 1928 von Courant, Lewy und Friedrichs veröffentlichten Arbeit “Über die partiellen Differenzengleichungen der mathematischen Physik” eingeführt, um für einige typische Beispiele nichtlinearer partieller Differentialgleichungen zu beweisen, dass die Lösungen der Differenzengleichung gegen die Lösung der entsprechenden Differentialgleichung konvergieren. Damit erhielten sie insbesondere einfache Beweise für die Lösbarkeit der Differentialgleichungen, die zwar in den meisten Beispielen schon bekannt war, aber zuvor mit uneinheitlichen und nicht verallgemeinerungsfähigen Methoden bewiesen. Courant und seinen Koautoren ging es dabei also weniger um die praktische Anwendung numerischer Verfahren als um Beweise für die Existenz von Lösungen. Die Fehleranalyse für Differenzenschemata elliptischer Gleichungen begann erst 1930 mit Gerschgorin (für die Poisson-Gleichung).
Anfänge digitaler Berechnungen
Während des zweiten Weltkrieges arbeiteten die in Deutschland gebliebenen Mathematiker an vorgeblich kriegswichtigen Problemen, in Wirklichkeit meist an theoretischen Untersuchungen zu Differentialgleichungen, nach dem Krieg kehrten die meisten sofort zur reinen Mathematik zurück. Hingegen kam zunächst kaum einer der Emigranten zurück. Anders als in Deutschland hatten in den USA Mathematiker und Naturwissenschaftler, oft aus Europa geflüchtet, eine wesentliche Rolle bei der Entwicklung neuer Waffen gespielt.
Anfang der 1940er Jahre hatte man begonnen, sich für digitale elektromagnetische Computer und deren Vorteile gegenüber mechanischen Rechnern zu interessieren. Fortschritte bei der Rechengeschwindigkeit waren zunächst nur durch bessere Röhrentechnik zu erzielen. Noch im Krieg hatte IBM die erste Maschine fertiggestellt. Die Rechenmaschine mit Vakuumröhren im Rechenwerk und mit auf Aussagenlogik beruhenden Schaltungen wurde beim Militär für lineare Differentialgleichungen und Integralgleichungen eingesetzt: der “Electrical Numerical Integrator and Computer”, kurz ENIAC, mit 17000 Radioröhren von 16 verschiedenen Typen, 30 mal 3 mal 1 Meter groß und mit einem Verbrauch von 140 Kilowatt und entsprechendem Kühlungsbedarf.

Man sah aber keine reale Möglichkeit, die die Speicherkapazität von Rechnern in einem Maße ausweiten würde wie es für die Behandlung nichtlinearer partieller Differentialgleichungen notwendig gewesen wäre. Viele Mathematiker hielten auch elektronische Konstruktionen für weniger zuverlässig als elektromechanische und lehnten sie deshalb ab trotz ihrer viel höheren Schnelligkeit.
Die Konstruktion einer solchen elektronischen Maschine wurde das Projekt John von Neumanns, der auf Einladung Oppenheimers seit 1943 beim Manhattan-Projekt in Los Alamos war. 1944/45 befaßte er sich mit den logischen Operationen – denen gegenüber er die elektronischen Aspekte als untergeordnet ansah – und wie diese Operationen von einer zentralen Stelle zu koordinieren seien. Ein theoretisches Konzept hatte schon 1936 Alan Turing entwickelt und von Neumanns Ideen waren eine konkrete Realisierung einer universellen Turingmaschine. In seinem Diskussionspapier "First Draft of a Report on the EDVAC“ definierte von Neumann in Analogie zum menschlichen Hirn eine Rechnerarchitektur aus Steuereinheit und arithmetischer Einheit sowie einer Speicher-einheit, welche Befehle seriell abarbeitet. Auf den dort dargestellten Ideen beruhten dann alle weiteren Entwicklungen von Rechnern, weshalb man von „von-Neumann-Architektur“ spricht. (Die Ingenieure Eckert und Mauchly, die Erbauer des ENIAC und des Nachfolgemodells EDVAC, sahen ihre Anteile später nicht genügend gewürdigt.)
Weil die ENIAC und ihre Nachfolger sehr wenig Speicherplatz für Zwischenresultate hatten, änderte sich die Ökonomie der Berechnungen über Nacht. Statt teurer Multiplikation und billigem Speicherplatz war jetzt die Multiplikation sehr billig und der Speicherplatz sehr teuer.
Neben den Grundlagen der Informatik beschäftigte sich von Neumann in der Nachkriegszeit auch mit den Grundlagen der Numerik. Seine 1947 mit Goldstine veröffentlichte Arbeit "Numerical inverting of matrices of high order“ wurde später als Beginn der numerischen linearen Algebra und überhaupt der modernen numerischen Mathematik angesehen, weil sie als eine der ersten Rundungsfehler und ihre Fortpflanzung diskutierte. In der Sache war sie hauptsächlich eine detaillierte Analyse der Rundungsfehler für Methoden der Faktorisierung und Inversion von Matrizen. Für invertierbare Matrizen A führte sie die Konditionszahl \( \kappa(A)=\Vert A\Vert \Vert A^{-1}\Vert \) ein und zeigte, dass die Algorithmen nur für gut konditionierte Probleme brauchbare Näherungslösungen liefern.
Die Arbeit war auch dadurch motiviert, dass unter angewandten Mathematikern divergierende Meinungen herrschten über die Zuverlässigkeit numerischer Verfahren zur Lösung linearer Gleichungssysteme, insbesondere auch des Gaußschen Eliminationsverfahrens für das numerische Invertieren von Matrizen. Als wichtigste Motivation nannten die Autoren aber, dass bisher nur Stabilitätsfragen untersucht worden seien und sie erstmals, und zwar an einem möglichst schwierigen Beispiel mit sehr vielen elementaren Operationen, die Konditionierung untersuchen wollten.
In der Einleitung ihrer Arbeit fassen sie ihre Ergebnisse so zusammen, dass zum Beispiel Matrizen der Ordnung 10, 15 oder 20 „meistens“ mit einer Genauigkeit von 8, 10 oder 12 weniger Ziffern als die Anzahl der Ziffern der Eingabe invertiert werden können. Mit „meistens“ meinen sie, dass unter Annahme einer plausiblen Wahrscheinlichkeits-verteilung auf den Matrizen diese Abschätzungen für alle Matrizen mit Ausnahme einer Minderheit geringer Wahrscheinlichkeit erfüllt sind. Diese Berechnungen fußten auf rigorosen individuellen Abschätzungen, die für alle Matrizen gültig sind. Mit einer wahrscheinlichkeitstheoretischen Behandlung der individuellen Matrizen hätten sie die Abschätzungen noch um einige Dezimalstellen verbessern können.
Wettervorhersagen und Computer in Princeton
Es wurde vor allem von Neumann zugeschrieben, dass die Mathematik bei der intellektuellen Elite der USA damals an Interesse gewann. Neben seiner Tätigkeit in Princeton hatte er zahlreiche Beraterposten inne. Später würde er seine Forschungstätigkeit aufgeben um Mitglied der Atomenergiekomission zu werden.

https://en.wikipedia.org/wiki/IAS_machine#/media/File:IAS_machine_at_Smithsonian.jpg
In der Nachkriegszeit gab es dann auch zeitweilig Computer am Institute for Advanced Study, obwohl man dort sonst keine experimentellen oder Ingenieurwissenschaften förderte. Es wurden vier Arbeitsgruppen gegründet: die Gruppe „Computer architecture und science“ sollte sich Gedanken über den grundsätzlichen Aufbau von Computern machen, eine weitere Gruppe beschäftigte sich mit numerischer Mathematik, eine andere, deren Arbeit schnell obsolet wurde, mit dem Entwurf und der Herstellung von Computern.
Die vierte Gruppe bekam die Aufgabe, ein Problem mit Computern zu bearbeiten, das man auch dem Laien und dem Politiker erklären konnte. So sollte die öffentliche Meinung für die Bereitstellung von Mitteln eingenommen werden. Von Neumann wählte als Problem für diese Gruppe die Meteorologie. 1950 entstand die erste im Computer berechnete Wettervorhersage, veröffentlicht unter dem Titel "Numerical Integration of the Barotropic Vorticity Equation" in der meteorologischen Fachzeitschrift Tellus. Ähnlich wie von Richardson vorgeschlagen hatten sie die Atmosphäre über Nordamerika mit 270 Gitterpunkten überdeckt und Finite-Differenzen-Methoden zur numerischen Lösung der Differentialgleichungen auf dem ENIAC verwandt. Die Rechenzeit für eine 24-Stunden-Vorhersage betrug recht genau 24 Stunden, wobei die meiste Zeit aber für manuelle Tätigkeiten mit den etwa 100.000 Lochkarten draufging. "Actually we estimate on the basis of the experiences acquired in the course of the Eniac calculations, that if a renewed systematic effort with the Eniac were to be made, and with a thorough routinization of the operations, a 24-hour prediction could be made on the Eniac in as little as 12 hours" (aus der Veröffentlichung von Charney, Fjörtoff und von Neumann).

Tatsächlich hatte von Neumann sich schon seit den 30er Jahren mit Problemen der Hydrodynamik beschäftigt und dadurch mit nichtlinearen partiellen Differentialgleichungen, die man nicht analytisch, sondern nur numerisch lösen konnte. (Insbesondere dann auch im Zusammenhang mit dem Manhattan-Projekt. Rechnungen zu Stoßwellen waren unter den ersten auf der ENIAC ausgeführten Berechnungen.)
In seiner November 1949 bei IBM vorgetragenen Ansprache "The future of high-Speed Computing“ benannte er vier Themen, für die man dauerhaft die immer schnelleren Computer benötigen würde, darunter als erstes die 2- und 3-dimensionalen Probleme der Hydrodynamik. Auf einer Tagung mit deutschen Wissenschaftsorganisatoren führte er zur mathematischen Behandlung meteorologischer Probleme aus:
In der mathematischen Behandlung der Meteorologie gibt es mindestens zwei Methoden, mit denen man das Problem angreifen kann. Die eine beruht auf sehr genauen statistischen Analysen der Vergangenheit und zielt darauf hin, die aus diesen abgeleiteteten Korrelationen auf die Zukunft anzuwenden. […] Bei der anderen Methode geht man dynamisch vor. Die Atmosphäre ist ja schließlich und endlich eine Flüssigkeit, und man kann ausrechnen, was sie tun wird […]
Mathematisch wandte er eine von Courant, Friedrichs und Lewy entwickelte Methode, mit der diese die Stabilität und Konvergenz der Finite-Differenzen-Methode bewiesen hatten um daraus rigorose Existenzsätze für gewöhnliche Differentialgleichungen herzuleiten, auf partielle Differentialgleichungen an und entwickelte heuristische Methoden für deren Stabilitätsanalyse.
Numerik der Navier-Stokes-Gleichungen
Mathematisch beruht die Klima- und Wetterforschung auf den Gleichungen der Hydrodynamik für die Strömung von linear-viskosen Flüssigkeiten und Gasen, den Navier-Stokes-Gleichungen. Olga Ladyzhenskaya hatte neben oder eher als Teil ihrer theoretischen Arbeiten schon seit Beginn der 50er Jahre auch an der Entwicklung von Differenzenschemata für verschiedene hyperbolische Gleichungen gearbeitet. 1959 bewies sie die globale eindeutige Lösbarkeit und die Glattheit der Lösungen für die 2-dimensionalen Navier-Stokes-Gleichungen und auch für die schwierigeren Euler-Gleichungen. (Dieselbe Frage für die 3-dimensionalen Navier-Stokes-Gleichungen, die ein mathematisches Modell der Strömung von linear-viskosen newtonschen Flüssigkeiten und Gasen sind, ist bekanntlich bis heute offen und eines der sieben Millennium-Probleme des Clay-Instituts.) Ihr Existenzbeweis für Lösungen der 2-dimensionalen Navier-Stokes-Gleichungen von 1959 beruhte aber auf den Methoden der Funktionalanalysis, dem Rieszschen Darstellungssatz und dem Fixpunktsatz von Leray und Schauder (zunächst zur Konstruktion schwacher Lösungen, deren Regularität dann mit Methoden von Golovkin und Solonnikov bewiesen wird). In der zweiten Hälfte der 60er Jahre entwickelte sie dann eine Reihe von Differenzenschemata für die 2- und 3-dimensionalen Navier-Stokes-Gleichungen. In der Arbeit "Устойчивые разностные схемы для уравнений Навье–Стокса” in Зап. научн. сем. ЛОМИ gelang es ihr 1969 erstmals, die Konvergenz solcher Schemata für Navier-Stokes-Gleichungen rigoros zu beweisen. Bei allen diesen Schemata gab sie den Beweisweg zum Nachweis der starken Konvergenz der Schemata in der Norm an, mit Einschluß der ersten Ableitungen, wodurch sie auch eine Methode zur Gewinnung von Abschätzungen der Konvergenzgeschwindigkeit erhielt. Mehr Informationen findet man bei MacTutor History oder in dem Artikel „Olga Ladyzhenskaya A Life-Long Devotion to Mathematics“ von Michael Struwe (in "Geometric analysis and nonlinear partial differential equations", Springer 2003).
Es wäre hier nicht der Platz, um über die Bedeutung der Strömungsmechanik und insbesondere der Navier-Stokes-Gleichung in der nicht-numerischen Mathematik zu schreiben. Eine neue Entwicklung, über die sogar Tageszeitungen wie Der Standard ausführlich berichteten, ist der im März auf dem ArXiv erschienene Preprint „ Hilbert's sixth problem: derivation of fluid equations via Boltzmann's kinetic theory“ von Yu Deng, Zaher Hani und Xiao Ma, in dem die kompressible Euler- und inkompressible Navier-Stokes-Gleichung rigoros aus Boltzmanns kinetischer Theorie für elastische Stöße von Systemen harter Kugeln hergeleitet werden.
Supercomputer
Es wäre ein Thema für einen eigenen Artikel, den Einfluss der Klimaforschung auf die angewandte Mathematik und insbesondere die numerische Strömungsmechanik der letzten Jahrzehnte zu erörtern. In Deutschland erhielt beispielsweise 2003 Rupert Klein den Leibniz-Preis für seine Arbeiten zur angewandten und numerischen Mathematik: <em>“ Von seinen gegenwärtigen Arbeitsschwerpunkten in Potsdam ist die Herleitung völlig neuartiger Mehrskalen-Modelle für die tropische Meteorologie hervorzuheben. Diese Modelle beschreiben die Wechselwirkung mesoskaliger Wolkenbildung und Konvektion mit Gravitations- und Schwerewellen. Dies kann für die Wettervorhersage und Klimaforschung wichtig sein. In der Atmosphäre spielen das hydrostatische und geostrophische Gleichgewicht je nach betrachteten Längenskalen eine zentrale Rolle. Für die Wettervorhersage interessieren aber die Abweichungen von diesen Gleichgewichten.“</em> (aus der Begründung auf der Webseite der DFG)
Laut dem Wikipedia-Artikel “Wettervorhersage” ist heute die Wettervorhersage ohne leistungsfähige Rechner undenkbar, in den 1950er und 1960er Jahren sei die Meteorologie die treibende Kraft hinter dem Bau der ersten Supercomputer gewesen. Von der Computertechnik her interessant sei, dass bei der Wetterprognose die identischen Rechenschritte unzählige Male ausgeführt werden müssen – nämlich für jedes der Kompartimente einmal. Somit eigneten sich Parallelrechner, welche Operationen gleichzeitig (parallel) anstelle nacheinander (seriell) durchführen, besonders für die Wettervorhersage. Da aber die Geschwindigkeit der einzelnen Computer-Prozessoren seit den 2010er Jahren kaum noch erhöht werden könne, verfügten die leistungsfähigsten Computer der Welt ohnehin über Tausende von Prozessoren bzw. Prozessorkerne, die gleichzeitig an denselben Aufgaben rechnen.
Ebenfalls laut dem Wikipedia-Artikel wurde die Bedeutung von Supercomputern und einer ausreichenden Datengrundlage durch den Hurrikan Sandy (2012) unterstrichen: "Während der amerikanische National Weather Service auf einem Rechner verschiedene Prognosemodelle betrieb, besaß das europäische ECMWF ein leistungsfähigeres Rechenzentrum, welches nur mit einem Modell arbeitete. Während das ECMWF bereits sieben Tage vorher – und mit geringer Irrtumswahrscheinlichkeit – prognostizieren konnte, dass der Hurrikan aufs amerikanische Festland stoßen wird, hielt das Modell des NWS dies für unwahrscheinlich. Dank dem besseren ECMWF-Modell konnte die Katastrophenwarnung wesentlich früher herausgegeben werden, allerdings haben spätere Berechnungen gezeigt, dass das ECMWF-Modell ohne die Daten der polaren Wettersatelliten zum selben Ergebnis wie der NWS gekommen wäre.“
Offensichtlich sind die numerischen Berechnungen nicht möglich ohne die Unmengen an Meßdaten, die täglich rund um den Globus erhoben werden. Es ist natürlich immer eine politische Entscheidung, welche Konsequenzen man aus den Messungen und den daraus berechneten Prognosen der Klimaforschung zieht. Man kann sich, wenn eine demokratisch legitimierte Mehrheit das so möchte, natürlich auch dafür entscheiden, Überschwemmungen, Dürren und Hurrikane als Preis für die weitere Verwendung fossiler Brennstoffe einzupreisen und mit diesen Folgen irgendwie fertigzuwerden. Absurd ist aber, wie es aktuell offensichtlich angestrebt wird, die Messung von Wetter- und Klimadaten und damit die auf diesen aufbauenden Prognosen zu unterbinden.
Aktuelles Beispiel (Präsidentendekret vom 23. Juni) ist die Kürzung fast aller Gelder für die US-Atmosphären-behörde NOAA, womit voraussichtlich die Messstation auf dem Mauna Loa in Hawaii geschlossen werden muss und damit die längste kontinuierliche Zeitreihe an CO2-Messungen (laufend seit 1958) unterbrochen würde.
Viele andere Messungen dürften von den dekretierten Kürzungen betroffen sein. Jochem Marotzke, Direktor des MPI für Meteorologie, nennt im Interview auf https://www.mpg.de/24345005/klimaforschung-usa-trump-regierung das Messprogramm Argo, "das für die Klimaforschung sehr wichtig ist. Es wurde von zwei US-Wissenschaftlern initiiert und zu mehr als 50 Prozent von den USA finanziert – durch NOAA. Es geht um 4200 Bojen, die durch die Ozeane driften und den Wärmeinhalt des Meeres messen. Mit der Temperatur an der Erdoberfläche, den Niederschlagsmengen und dem Meeresspiegel ist das eine der wichtigsten Größen im Klimasystem, weil über 90 Prozent der Energie, die durch den menschengemachten Treibhauseffekt im Erdsystem zurückgehalten wird, in die Ozeane geht. Wenn es NOAA jetzt an den Kragen geht, ist Argo in höchster Gefahr, weil die Bojen alle fünf Jahre ausgetauscht und jedes Jahr etwa 800 neue ausgesetzt werden müssen. Man kann sich aus rein ökonomischen Gründen durchaus fragen, warum die USA über 50 Prozent übernehmen müssen. Aber das ist ein Beispiel dafür, wie entschlossen die USA lange auch in der Klimaforschung die Führungsrolle übernommen haben und wie bewunderns-wert viel da investiert wurde.“
Ein Einstellen der Messungen und eine Löschung von Daten behindert natürlich nicht nur die Klimaforschung, sondern auch gewöhnliche Wettervorhersagen oder beispielsweise die Vorhersage von Sturzfluten oder Tornados. Andere Länder werden sich auch in dieser Frage von den USA unabhängig machen müssen.
Man hat inzwischen damit begonnen, wissenschaftliche Daten (nicht nur der Klimaforschung) auch auf europäischen Servern zu speichern, zum Beispiel hat das Leibniz-Informationszentrum Hannover im Juni in zehntägiger Arbeit ein Backup aller 2,7 Millionen Arbeiten auf dem ArXiv angelegt. Erheblich aufwendiger und teurer wird es werden, wenn in Zukunft auch die Erhebung neuer Wetter- und Klimadaten ohne Beteiligung der USA durchgeführt werden muss.