Wer erinnert sich noch? von Kevin Fox via Google Blogoscoped (gefunden in den Folien zu Tao's Mahler-Vorlesung, über die ich hier geschrieben habe) Morgen hat Google übrigens offiziell 11. Geburtstag. Eine Alpha-Version (hier zu besichtigen) hatte es aber schon ab 1997 gegeben.

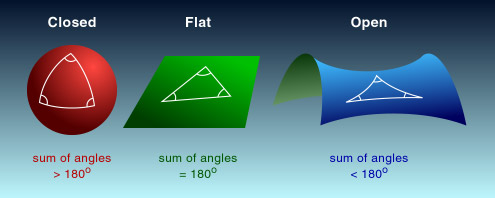
Dicke und dünne Dreiecke.In TvF 56 hatten wir mal über Geodäten geschrieben, kürzeste Verbindungskurven wie Geraden in der (euklidischen) Ebene oder Großkreise auf der Sphäre. In der Ebene gibt es (anders als auf der Sphäre) nur eine kürzeste Verbindung zwischen zwei Punkten. Wie letzte Woche erwähnt, ist dies auf...

Wie im vorigen Beitrag geschrieben, ist am Mittwoch der Preprint von Hill-Hopkins-Ravenel zur Kervaire-Vermutung auf dem ArXiv erschienen. Eine der Anwendungen, die sich daraus ergeben, ist die Klassifikation 'exotischer Sphären'.Stetigkeit und DifferenzierbarkeitIm ersten Semester oder schon in der Schule lernt man...

Am Mittwoch ist der seit April avisierte Preprint von Hill-Hopkins-Ravenel zur Kervaire-Vermutung auf dem ArXiv erschienen. Der Beweis war im April auf der Atiyah80-Konferenz angekündigt worden (wir hatten hier und hier berichtet). Die Kervaire-Vermutung gilt als das schwierigste ungelöste Problem der...

Nachteilig an einer künstlichen Begradigung bzw. zu straffen Flussregulierung ist, dass sich stromabwärts die Überschwemmungsgefahr verstärkt. (Wikipedia)In TvF 56 und letzte Woche hatten wir über Geodäten geschrieben, lokal kürzeste Verbindungskurven wie zum Beispiel Geraden in der (euklidischen) Ebene oder...