Topologie von Flächen XVII
Coca-Cola macht aus Anlaß der EM gerade Werbung mit einer
Flasche im Fußballmuster. Dabei hat man sich aber etwas vertan. Statt, wie es bei einem
klassischen Fußball sein müßte, mit 5- und 6-Ecken zu pflastern, verwendet der Coca-Cola-Fußball nur 6-Ecke.
Das ist aber, wie wir
letzte Woche ausführlich bewiesen hatten, überhaupt nicht möglich: jede Landkarte der Sphäre hat mindestens ein 5- oder 4- oder 3-Eck. Es gibt keine Zerlegung der Sphäre in lauter 6-Ecke. (Daraus hatten wir letzte Woche hergeleitet, daß sich jede Landkarte auf der Sphäre mit 6 Farben färben läßt. Mit erheblich mehr Computer-Aufwand, kann man zeigen, daß sich jede Landkarte auf der Sphäre sogar mit 4 Farben färben läßt.)
Überraschenderweise ist es nur auf der Sphäre schwierig, optimale Färbungen zu finden. Für Landkarten auf einem Torus weiß man schon lange, daß man immer mit 7 Farben auskommt, und wie die folgenden beiden Beispiele zeigt, gibt es auf dem Torus Landkarten mit 7 Ländern, so daß jedes Land mit jedem der 6 anderen eine gemeinsame Grenze hat. (Damit braucht man 7 unterschiedliche Farben.)
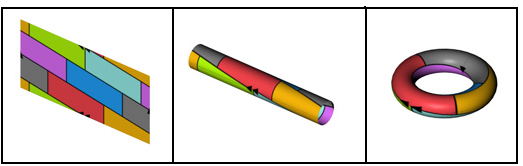

Der Beweis des 7-Farben-Satzes für den Torus ist sehr ähnlich zum Beweis des 6-Farben-Satzes für die Sphäre. Der einzige Unterschied ist, daß die Euler'sche Polyederformel für den Torus E-K+F=0 (nicht =2) ergibt (
Teil 3,
Teil 6).
Jede Landkarte auf dem Torus kann mit 7 Farben gefärbt werden.
Beweis:
Wir zeigen zunächst, daß es ein Land mit höchstens 6 Nachbarn gibt.
Wenn wir die Länder als (krummlinige) Vielecke auffassen, und mit E,F,K die Gesamtzahl der Ecken, Kanten, Flächen bezeichnen, dann ist E-K+F=0.
Andererseits ist 3E≤2K, weil jede Kante 2 Ecken hat, aber an jeder Ecke mindestens 3 Kanten zusammenkommen. Wenn jedes Land mindestens 7 Nachbarn hätte, d.h. jede Fläche mindestens 7 Kanten hätte (und natürlich jede Kante zu 2 Flächen gehört), dann wäre 2F≤7K. Damit ergibt sich aber der Widerspruch
0=E-K+F ≤ 2/3 K - K + 2/7 K=-1/21 K < 0.
Wegen diesem Widerspruch muß es also in jeder Karte mindestens ein Land mit höchstens 6 Nachbarn geben.
Jetzt führen wir den Beweis des 7-Farben-Satzes durch vollständige Induktion nach Anzahl der Länder. Induktionsanfang (Karte mit 1 Land) ist offensichtlich. Sei der Satz bewiesen für Karten mit n Ländern.
Sei jetzt eine Karte mit n+1 Ländern gegeben. Wir wissen, daß es ein Land mit höchstens 6 Nachbarn gibt. Wenn wir dieses Land weglassen (genauer: dieses Land auf seinen Mittelpunkt zusammenziehen und die benachbarten Ländern entsprechend etwas ausdehnen), bekommen wir eine Karte mit n Ländern, die sich nach Induktionsvoraussetzung mit 7 Farben färben läßt. Weil das (n+1)-te Land höchstens 6 Nachbarn hat, bleibt eine der 7 Farben übrig, um dieses auch noch zu färben.
Auf ähnliche Weise kann man auch auf komplizierteren Flächen die minimale Zahl notwendiger Farben bestimmen.
Auf einer Fläche mit 2 Henkeln braucht man mindestens 8 Farben, auf einer Fläche mit 3 Henkeln mindestens 9 Farben, und auch für alle anderen Flächen gibt es eine
exakte Formel für die Mindestanzahl an Farben.
Noch ein Bild einer optimalen Färbung für das Möbiusband (
Teil 7) mit 6 Farben.
 Die letzten beiden Bilder sind von Manfred Börgens.
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16
Die letzten beiden Bilder sind von Manfred Börgens.
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16

 Der Beweis des 7-Farben-Satzes für den Torus ist sehr ähnlich zum Beweis des 6-Farben-Satzes für die Sphäre. Der einzige Unterschied ist, daß die Euler'sche Polyederformel für den Torus E-K+F=0 (nicht =2) ergibt (Teil 3, Teil 6).
Jede Landkarte auf dem Torus kann mit 7 Farben gefärbt werden.
Beweis: Wir zeigen zunächst, daß es ein Land mit höchstens 6 Nachbarn gibt.
Wenn wir die Länder als (krummlinige) Vielecke auffassen, und mit E,F,K die Gesamtzahl der Ecken, Kanten, Flächen bezeichnen, dann ist E-K+F=0.
Andererseits ist 3E≤2K, weil jede Kante 2 Ecken hat, aber an jeder Ecke mindestens 3 Kanten zusammenkommen. Wenn jedes Land mindestens 7 Nachbarn hätte, d.h. jede Fläche mindestens 7 Kanten hätte (und natürlich jede Kante zu 2 Flächen gehört), dann wäre 2F≤7K. Damit ergibt sich aber der Widerspruch
0=E-K+F ≤ 2/3 K - K + 2/7 K=-1/21 K < 0.
Wegen diesem Widerspruch muß es also in jeder Karte mindestens ein Land mit höchstens 6 Nachbarn geben.
Jetzt führen wir den Beweis des 7-Farben-Satzes durch vollständige Induktion nach Anzahl der Länder. Induktionsanfang (Karte mit 1 Land) ist offensichtlich. Sei der Satz bewiesen für Karten mit n Ländern.
Sei jetzt eine Karte mit n+1 Ländern gegeben. Wir wissen, daß es ein Land mit höchstens 6 Nachbarn gibt. Wenn wir dieses Land weglassen (genauer: dieses Land auf seinen Mittelpunkt zusammenziehen und die benachbarten Ländern entsprechend etwas ausdehnen), bekommen wir eine Karte mit n Ländern, die sich nach Induktionsvoraussetzung mit 7 Farben färben läßt. Weil das (n+1)-te Land höchstens 6 Nachbarn hat, bleibt eine der 7 Farben übrig, um dieses auch noch zu färben.
Auf ähnliche Weise kann man auch auf komplizierteren Flächen die minimale Zahl notwendiger Farben bestimmen.
Auf einer Fläche mit 2 Henkeln braucht man mindestens 8 Farben, auf einer Fläche mit 3 Henkeln mindestens 9 Farben, und auch für alle anderen Flächen gibt es eine exakte Formel für die Mindestanzahl an Farben.
Noch ein Bild einer optimalen Färbung für das Möbiusband (Teil 7) mit 6 Farben.
Der Beweis des 7-Farben-Satzes für den Torus ist sehr ähnlich zum Beweis des 6-Farben-Satzes für die Sphäre. Der einzige Unterschied ist, daß die Euler'sche Polyederformel für den Torus E-K+F=0 (nicht =2) ergibt (Teil 3, Teil 6).
Jede Landkarte auf dem Torus kann mit 7 Farben gefärbt werden.
Beweis: Wir zeigen zunächst, daß es ein Land mit höchstens 6 Nachbarn gibt.
Wenn wir die Länder als (krummlinige) Vielecke auffassen, und mit E,F,K die Gesamtzahl der Ecken, Kanten, Flächen bezeichnen, dann ist E-K+F=0.
Andererseits ist 3E≤2K, weil jede Kante 2 Ecken hat, aber an jeder Ecke mindestens 3 Kanten zusammenkommen. Wenn jedes Land mindestens 7 Nachbarn hätte, d.h. jede Fläche mindestens 7 Kanten hätte (und natürlich jede Kante zu 2 Flächen gehört), dann wäre 2F≤7K. Damit ergibt sich aber der Widerspruch
0=E-K+F ≤ 2/3 K - K + 2/7 K=-1/21 K < 0.
Wegen diesem Widerspruch muß es also in jeder Karte mindestens ein Land mit höchstens 6 Nachbarn geben.
Jetzt führen wir den Beweis des 7-Farben-Satzes durch vollständige Induktion nach Anzahl der Länder. Induktionsanfang (Karte mit 1 Land) ist offensichtlich. Sei der Satz bewiesen für Karten mit n Ländern.
Sei jetzt eine Karte mit n+1 Ländern gegeben. Wir wissen, daß es ein Land mit höchstens 6 Nachbarn gibt. Wenn wir dieses Land weglassen (genauer: dieses Land auf seinen Mittelpunkt zusammenziehen und die benachbarten Ländern entsprechend etwas ausdehnen), bekommen wir eine Karte mit n Ländern, die sich nach Induktionsvoraussetzung mit 7 Farben färben läßt. Weil das (n+1)-te Land höchstens 6 Nachbarn hat, bleibt eine der 7 Farben übrig, um dieses auch noch zu färben.
Auf ähnliche Weise kann man auch auf komplizierteren Flächen die minimale Zahl notwendiger Farben bestimmen.
Auf einer Fläche mit 2 Henkeln braucht man mindestens 8 Farben, auf einer Fläche mit 3 Henkeln mindestens 9 Farben, und auch für alle anderen Flächen gibt es eine exakte Formel für die Mindestanzahl an Farben.
Noch ein Bild einer optimalen Färbung für das Möbiusband (Teil 7) mit 6 Farben.
 Die letzten beiden Bilder sind von Manfred Börgens.
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16
Die letzten beiden Bilder sind von Manfred Börgens.
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16 


