Integral-Berechnung mit Hilfe stetiger Deformationen.
Eine der ursprünglichen Anwendungen der Topologie war bei der Berechnung von Integralen. Wir hatten
letzte Woche begonnen, dies am Beispiel cos(x)/(x
2+1) auszuführen.
Statt das Integral dieser Funktion über die reellen Zahlen zu berechnen (was man eigentlich möchte), kann man auch das Integral der Funktion über die folgende geschlossene Kurve in der komplexen Zahlenebene
C berechnen (und bekommt denselben Wert, siehe
TvF XXV):
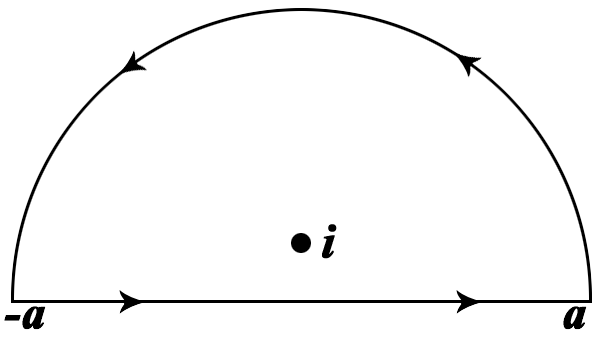
A priori hat man natürlich nichts gewonnen, wenn man jetzt statt des Integrals über die reellen Zahlen das Integral über eine Kurve in der komplexen Zahlenebene berechnen muß. Der Punkt ist der folgende Satz, der besagt, daß man Kurven deformieren kann ohne den Wert des Integrals zu ändern. (Diese Flexibilität erleichtert die Berechnung.)
Integralsatz von Cauchy: Sei f eine auf einer Teilmenge A von C komplex-differenzierbare Funktion. Wenn K und L zwei homotope Kurven in A sind, dann stimmen die Integrale von f über den Kurven K und L überein.
Zur Erinnerung (
TvF XXII): "homotop" hieß, daß sich die Kurve K stetig in die Kurve L deformieren läßt (ohne die Menge A zu verlassen).
Insbesondere heißt das für eine auf ganz
C komplex-differenzierbare Funktion (wie z.B. f(z)=z oder f(z)=z
2 usw.), daß das Integral über jede
geschlossene Kurve einfach 0 ist. (Weil jede Kurve in der Ebene sich stetig auf einen Punkt zusammenziehen läßt.) Aber auf cos(z)/(z
2+1) kann man dies nicht anwenden, weil es in
i oder
-i nicht differenzierbar ist.
Mit diesem Satz kann man oft Integrale berechnen: man deformiert einfach die Kurve in eine geeignete Kurve, für die sich das Integral einfacher berechnen läßt.
Ein Beispiel: man will f(z)=1/z über eine Kurve integrieren will, die einmal um den Nullpunkt herumläuft. f ist in 0 nicht definiert, sonst aber überall komplex-differenzierbar. Es sind also Deformationen der Kurve erlaubt, die nicht durch 0 gehen. Zum Beispiel kann man die Kurve in den Kreis um 0 mit Radius 1 deformieren. Für diesen kann man das Integral leicht berechnen. Es ist
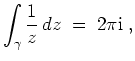
womit (nach Cauchy's Integralsatz) dasselbe Ergebnis dann also auch für jede andere Kurve gilt, die einmal um 0 herumläuft.
Analog berechnet man (für m=2,3,4,...)
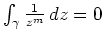
für jede Kurve, die einmal um 0 herumläuft.
Und wenn man irgendeine Funktion hat, die nur in 0 nicht differenzerbar ist, entwickelt man sie in eine sogenannte Laurentreihe f(z)=a
nz
n+...+a
1z+a
0+a
-1/z+a
-2/z
2+... und erhält (mit den beiden Formeln oben) als Integral 2πia
-1, denn das Integral aller anderen Summanden außer a
-1/z ist ja 0. (Dies ist der sogenannte Residuensatz, sicher einer der meistangewandten mathematischen Sätze. Denn Integrale muß man ja überall berechnen, von der Wahrscheinlichkeitstheorie bis zum Ingenieurwesen.)
Um zum ursprünglichen Problem der Integration von cos(z)/(z
2+1) bzw. e
iz/(z
2+1) zurückzukommen: hier kann man den Residuensatz nicht direkt anwenden, weil diese Funktion in
i (statt in 0) nicht definiert ist. (Außerdem ist sie in
-i nicht definiert. Das stört hier aber nicht, weil
-i nicht im Inneren der Kurve liegt.)
Statt einer Laurentreihe mit Variable z brauchen wir also eine Laurentreihe mit Variable (z-i). Diese kann man berechnen, und als Faktor a
-1 vor 1/(z-i) erhält man e
i*i/2i. Für den Wert des Integrals bekommt man also 2πia
-1=πcos(i)=
π(e+1/e)/2 π/e für das Integral von e
iz/(z
2+1) und damit auch für das Integral des Realteils cos z/(z
2+1).
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17, Teil 18, Teil 19, Teil 20, Teil 21, Teil 22, Teil 23, Teil 24, Teil 25
 A priori hat man natürlich nichts gewonnen, wenn man jetzt statt des Integrals über die reellen Zahlen das Integral über eine Kurve in der komplexen Zahlenebene berechnen muß. Der Punkt ist der folgende Satz, der besagt, daß man Kurven deformieren kann ohne den Wert des Integrals zu ändern. (Diese Flexibilität erleichtert die Berechnung.)
Integralsatz von Cauchy: Sei f eine auf einer Teilmenge A von C komplex-differenzierbare Funktion. Wenn K und L zwei homotope Kurven in A sind, dann stimmen die Integrale von f über den Kurven K und L überein.
Zur Erinnerung (TvF XXII): "homotop" hieß, daß sich die Kurve K stetig in die Kurve L deformieren läßt (ohne die Menge A zu verlassen).
Insbesondere heißt das für eine auf ganz C komplex-differenzierbare Funktion (wie z.B. f(z)=z oder f(z)=z2 usw.), daß das Integral über jede geschlossene Kurve einfach 0 ist. (Weil jede Kurve in der Ebene sich stetig auf einen Punkt zusammenziehen läßt.) Aber auf cos(z)/(z2+1) kann man dies nicht anwenden, weil es in i oder -i nicht differenzierbar ist.
Mit diesem Satz kann man oft Integrale berechnen: man deformiert einfach die Kurve in eine geeignete Kurve, für die sich das Integral einfacher berechnen läßt.
Ein Beispiel: man will f(z)=1/z über eine Kurve integrieren will, die einmal um den Nullpunkt herumläuft. f ist in 0 nicht definiert, sonst aber überall komplex-differenzierbar. Es sind also Deformationen der Kurve erlaubt, die nicht durch 0 gehen. Zum Beispiel kann man die Kurve in den Kreis um 0 mit Radius 1 deformieren. Für diesen kann man das Integral leicht berechnen. Es ist
A priori hat man natürlich nichts gewonnen, wenn man jetzt statt des Integrals über die reellen Zahlen das Integral über eine Kurve in der komplexen Zahlenebene berechnen muß. Der Punkt ist der folgende Satz, der besagt, daß man Kurven deformieren kann ohne den Wert des Integrals zu ändern. (Diese Flexibilität erleichtert die Berechnung.)
Integralsatz von Cauchy: Sei f eine auf einer Teilmenge A von C komplex-differenzierbare Funktion. Wenn K und L zwei homotope Kurven in A sind, dann stimmen die Integrale von f über den Kurven K und L überein.
Zur Erinnerung (TvF XXII): "homotop" hieß, daß sich die Kurve K stetig in die Kurve L deformieren läßt (ohne die Menge A zu verlassen).
Insbesondere heißt das für eine auf ganz C komplex-differenzierbare Funktion (wie z.B. f(z)=z oder f(z)=z2 usw.), daß das Integral über jede geschlossene Kurve einfach 0 ist. (Weil jede Kurve in der Ebene sich stetig auf einen Punkt zusammenziehen läßt.) Aber auf cos(z)/(z2+1) kann man dies nicht anwenden, weil es in i oder -i nicht differenzierbar ist.
Mit diesem Satz kann man oft Integrale berechnen: man deformiert einfach die Kurve in eine geeignete Kurve, für die sich das Integral einfacher berechnen läßt.
Ein Beispiel: man will f(z)=1/z über eine Kurve integrieren will, die einmal um den Nullpunkt herumläuft. f ist in 0 nicht definiert, sonst aber überall komplex-differenzierbar. Es sind also Deformationen der Kurve erlaubt, die nicht durch 0 gehen. Zum Beispiel kann man die Kurve in den Kreis um 0 mit Radius 1 deformieren. Für diesen kann man das Integral leicht berechnen. Es ist
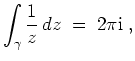 womit (nach Cauchy's Integralsatz) dasselbe Ergebnis dann also auch für jede andere Kurve gilt, die einmal um 0 herumläuft.
Analog berechnet man (für m=2,3,4,...)
womit (nach Cauchy's Integralsatz) dasselbe Ergebnis dann also auch für jede andere Kurve gilt, die einmal um 0 herumläuft.
Analog berechnet man (für m=2,3,4,...)
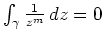 für jede Kurve, die einmal um 0 herumläuft.
Und wenn man irgendeine Funktion hat, die nur in 0 nicht differenzerbar ist, entwickelt man sie in eine sogenannte Laurentreihe f(z)=anzn+...+a1z+a0+a-1/z+a-2/z2+... und erhält (mit den beiden Formeln oben) als Integral 2πia-1, denn das Integral aller anderen Summanden außer a-1/z ist ja 0. (Dies ist der sogenannte Residuensatz, sicher einer der meistangewandten mathematischen Sätze. Denn Integrale muß man ja überall berechnen, von der Wahrscheinlichkeitstheorie bis zum Ingenieurwesen.)
Um zum ursprünglichen Problem der Integration von cos(z)/(z2+1) bzw. eiz/(z2+1) zurückzukommen: hier kann man den Residuensatz nicht direkt anwenden, weil diese Funktion in i (statt in 0) nicht definiert ist. (Außerdem ist sie in -i nicht definiert. Das stört hier aber nicht, weil -i nicht im Inneren der Kurve liegt.)
Statt einer Laurentreihe mit Variable z brauchen wir also eine Laurentreihe mit Variable (z-i). Diese kann man berechnen, und als Faktor a-1 vor 1/(z-i) erhält man ei*i/2i. Für den Wert des Integrals bekommt man also 2πia-1=πcos(i)=
für jede Kurve, die einmal um 0 herumläuft.
Und wenn man irgendeine Funktion hat, die nur in 0 nicht differenzerbar ist, entwickelt man sie in eine sogenannte Laurentreihe f(z)=anzn+...+a1z+a0+a-1/z+a-2/z2+... und erhält (mit den beiden Formeln oben) als Integral 2πia-1, denn das Integral aller anderen Summanden außer a-1/z ist ja 0. (Dies ist der sogenannte Residuensatz, sicher einer der meistangewandten mathematischen Sätze. Denn Integrale muß man ja überall berechnen, von der Wahrscheinlichkeitstheorie bis zum Ingenieurwesen.)
Um zum ursprünglichen Problem der Integration von cos(z)/(z2+1) bzw. eiz/(z2+1) zurückzukommen: hier kann man den Residuensatz nicht direkt anwenden, weil diese Funktion in i (statt in 0) nicht definiert ist. (Außerdem ist sie in -i nicht definiert. Das stört hier aber nicht, weil -i nicht im Inneren der Kurve liegt.)
Statt einer Laurentreihe mit Variable z brauchen wir also eine Laurentreihe mit Variable (z-i). Diese kann man berechnen, und als Faktor a-1 vor 1/(z-i) erhält man ei*i/2i. Für den Wert des Integrals bekommt man also 2πia-1=πcos(i)=


