"Nun ist die Frage generaliter: da ein polygonum von n Seiten durch n-3 diagonales in n-2 triangula zerschnitten wird, auf wie vielerley verschiedene Arten solches geschehen könne." (Euler an Goldbach) Letzte Woche hatten wir beschrieben, wie man verschiedene Flächen in Dreiecke zerlegen ("triangulieren") kann. Passend dazu ist mir diese Woche in der Bibliothek gerade das neue Buch Loera-Rambau-Santos:"Triangulations" aufgefallen, in dem es zwar kaum um Topologie (sondern eher um Polytope und z.B. auch um Triangulierungen der Ebene) geht, aber dessen erstes Kapitel hier doch ganz gut als Einschub passt, bevor es nächste Woche wieder mit dem Schönflies-Theorem und Triangulierungen weitergeht. Letzte Woche hatten wir z.B. Triangulierungen des 4-oder 8-Ecks benutzt, mit denen wir dan Triangulierungen des Torus bzw. der Brezel bekamen. Man kann sich dann natürlich fragen, wieviele verschiedene Möglichkeiten es dafür gibt, also wieviel verschiedene Triangulierungen des 4- oder 8-Ecks, oder allgemein des n-Ecks. Diese Frage wird, quasi zum Aufwärmen, in Kapitel 1.1. des Buches von Loera-Rambau-Santos beantwortet. Die Triangulierungen des 4-Ecks kann man leicht abzählen - es gibt 2 (nämlich 2 Möglichkeiten, eine Diagonale einzuzeichnen). Für das Fünfeck gibt es 5 Möglichkeiten: und für das Sechseck 14: 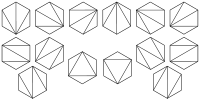Sei t_n die Anzahl der Triangulierungen eines n-Ecks, man hat also t₂=t₃=1, t₄=2, t₅=5, t₆=14. Es gibt dann verschiedene Möglichkeiten, eine Rekursionsformel zu bauen. Die naheliegende: Eine Kante des n-Ecks muss in einem Dreieck der Triangulierung vorkommen. Je nachdem, welches die dritte Ecke dieses Dreiecks ist, wird das n-Eck für irgendein k in ein k-Eck und ein n+1-k-Eck zerlegt, die dann einzeln trianguliert werden. Also t_n=t₂t_n-1+t₃t_n-2+t₄t_n-3+...+t_n-1t₂ Damit kann man im Prinzip induktiv alle t_n ausrechnen, eine geschlossene Formel für t_n erkennt man aber nicht auf Anhieb. Besser ist deshalb ein nicht so offensichtlicher Zugang des doppelten Abzählens: man kann ja eine Triangulierung des n-Ecks durch "Verdoppeln" einer Kante zu einer Triangulierung des n+1-Ecks machen (dafür gibt es 2(2n-3) Möglichkeiten, nämlich 2 zu jeder der 2n-3 Kanten der Triangulierung) und umgekehrt eine Triangulierung des n+1-Ecks durch "Kontraktion" einer Kante zu einer Triangulierung des n-Ecks machen. Dabei gibt es jeweils n Triangulierungen des n+1-Ecks, die sich durch Kontraktion in eine gegebene Triangulierung des n-Ecks vereinfachen lassen. Also 2(2n-3)t_n=nt_n+1. Mit dieser Rekursion bekommt man dann sofort eine geschlossene Formel für t_n: t_n ist gerade die Catalan-Zahl C_n-2. (Nebenbei: die geschlossene Formel stammt aus einem beim Euler-Archiv online-stehenden Brief von Euler an Goldbach vom 4.9.1751.) Die Catalan-Zahlen kommen übrigens in der Mathematik noch an vielen anderen Stellen vor (vgl. auch den Wikipedia-Artikel), z.B. als Anzahl der Binärbäume mit n+1 Ecken, oder als Anzahl der eindimensionalen Irrfahrten von 0 nach 2n mit Anfangs- und Endpunkt in 0, so dass sich der Pfad nie unterhalb der x-Achse befindet, oder als Anzahl der Möglichkeiten, n+1 Faktoren zu klammern:

((ab)c)d (a(bc))d (ab)(cd) a((bc)d) a(b(cd))

In Kapitel 1.1. von Loera-Rambau-Santos werden einige dieser Gleichheiten noch direkt bewiesen (also ohne explizites Ausrechnen der jeweiligen Anzahlen).

Um einen Kommentar zu verfassen, müssen Sie sich einloggen bzw. kurz als Gast registrieren.