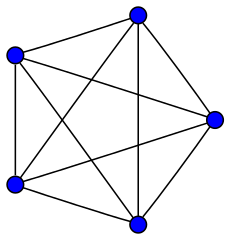
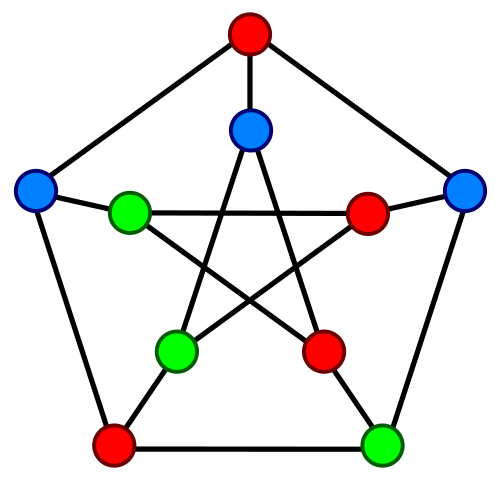
Im letzten Beitrag hatten wir über Färbungen von Graphen geschrieben und darüber, dass das chromatische Polynom stets unimodal ist, also seine Koeffizienten erst steigen und dann fallen. Zum Beispiel hat der vollständige Graph auf fünf Knoten K₅ das chromatische Polynom x⁵-10x⁴+35x³-50x²+24x oder der bipartite Graph K_2,3 das chromatische Polynom x⁵-6x⁴+15x³-17x²+7x oder der Petersen-Graph das Polynom x¹⁰-15x⁹+104x⁸-455x⁷+1353x⁶-2861x⁵+4275x⁴-4305x³+2706x²-704x. In einer nächsten Monat in den Annals of Mathematics erscheinenden Arbeit von Adiprasito, Huh und Katz wird nun gezeigt, dass dies ein Spezialfall eines allgemeineren Phänomens ist und allgemein für die chromatischen Polynome sogenannter Matroide gilt. Dahinter steckt eine Struktur, die in allen möglichen Zusammenhängen der Mathematik vorkommt und damit für viele in unterschiedlichen Zusammenhängen vorkommende unimodale Polynome verantwortlich ist: die sogenannten Lefschetz-Pakete. Die sind ursprünglich bekannt aus der komplexen Geometrie als eine bestimmte Struktur auf der Kohomologie nicht-singulärer projektiver Varietäten (und allgemeiner Kähler-Mannigfaltigkeiten): Poincaré-Dualität, schwerer Lefschetz-Satz und Hodge-Riemann-Relationen. Dieselben Strukturen gibt es auch auf der sogenannten Schnittkohomologie beliebiger Varietäten (mit Singularitäten). Seit den 40er Jahren waren die Weil-Vermutungen die größte offene Frage der algebraischen Geometrie. Sie besagen, dass man die Lösungen einer polynomiellen Gleichung modulo p^m (einer Primzahlpotenz) bestimmen kann, wenn man die algebraische Topologie (die Bettizahlen) derselben Gleichung über den komplexen Zahlen kennt. Zum Beispiel ist es nicht einfach die Anzahl der Lösungen von x³+y³+z³=0 modulo einer Primzahlpotenz zu berechnen. Über den komplexen Zahlen ist diese Kurve (in der projektiven Ebene) aber einfach ein Torus. Die Bettizahlen sind b₀=1,b₁=2,b₂=1. Mit den Weil-Vermutungen bekommt man dann zum Beispiel 9 Lösungen modulo 7, 63 Lösungen modulo 7², 324 Lösungen modulo 7³ und eine allgemeine Formel für die Lösungen modulo 7^m. Alexander Grothendieck hatte 1968 erkannt, dass man die Weil-Vermutungen herleiten könnte, wenn es es eine Struktur aus Poincaré-Dualität, schwerer Lefschetz-Satz und Hodge-Riemann-Relationen auch auf der Gruppe algebraischer Zykel (modulo homologischer Äquivalenz) in einer algebraischen Varietät gibt. Diese Vermutung wurde dann als Standardvermutung bekannt. Grothendieck verließ bald danach die Mathematik und für die Standardvermutung sind bis heute nicht viel mehr Beispiele bekannt als schon 1968. Die Weil-Vermutungen wurden 1974 von Grothendiecks früherem Schüler Pierre Deligne bewiesen, er benutzte aber statt der Standardvermutungen explizitere Methoden der Zahlentheorie (Modulformen), mit denen sich Grothendieck nicht im Geringsten auskannte. In Récoltes et Semailles beschwerte sich Grothendieck bitter darüber, dass seine Arbeit von seinen Schülern nicht fortgesetzt worden sei und diese die Schwierigkeiten einfach "umgangen" hätten. Während also die Standardvermutungen immer noch offen sind, hat man inzwischen dieselben Strukturen - Poincaré-Dualität, schwerer Lefschetz-Satz und Hodge-Riemann-Relationen - in vielen anderen Bereichen der Mathematik gefunden. Die bemerkenswertesten Beispiele sind vielleicht die Arbeiten von Elias und Williamson, die solche Strukturen in der Darstellungstheorie finden, und die erwähnte Arbeit von Adiprasito, Huh und Katz, die solche Strukturen in der Theorie der Matroide findet. Sowohl Williamson als auch Huh und Adiprasito werden übrigens immer wieder als Kandidaten für die Fields-Medaillen genannt, die nächste Woche in Rio de Janeiro vergeben werden. Diese Strukturen sind dann wiederum verantwortlich dafür, dass unimodale Polynome in so vielen unterschiedlichen Gebieten der Mathematik vorkommen. Grob gesagt folgt aus den Hodge-Riemann-Relationen die Positivität gewisser Determinanten, also Ungleichungen der Form a_i²-a_i+1a_i-1>0. Eine Folge von Null verschiedener Zahlen, die diese Ungleichung für alle i erfüllt, ist unimodal. Es gibt aber unimodale Polynome auch noch in vielen Bereichen der Mathematik, wo es noch keine Erklärung (und keinen Beweis) für die Unimodalität gibt. Zum Beispiel hat Stoimenow vermutet, dass das Alexanderpolynom von Knoten unimodal ist. Es deutet also vieles darauf hin, dass es Analoga zu Grothendiecks Standardvermutungen noch sehr viel allgemeiner in aller möglichen Mathematik geben könnte - irgendeine Metastruktur, die sich dann auf völlig verschiedene mathematische Strukturen anwenden ließe.

Um einen Kommentar zu verfassen, müssen Sie sich einloggen bzw. kurz als Gast registrieren.