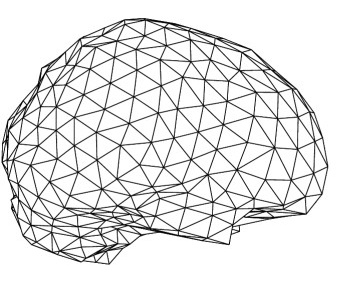
Flächen in Dreiecke zerlegen und der Satz von Schönflies.Ein wichtiges Hilfsmittel bei der Klassifikation von Flächen sind 'Triangulierungen', d.h. Zerlegungen der Fläche in Dreiecke (TvF 161): cis.jhu.edu/education/introPatternTheory/additional/curvature/curvature25.htmlFlächen sind ja eigentlich (TvF 159) dadurch...

Approximationen der Wirklichkeit.Heute ist der 22.7., der π-Approximationstag. Man beachte aber: 22/7=3,1428... ist nicht π=3,1415...:singingbanana.tumblr.com/post/7921183215/reposting-this-for-pi-approximation-dayFür die Nicht-Frankophonen: 'ceci n'est pas une pi' bedeutet 'das ist kein Pi', das Bild und der...

Images des Mathématiques hatte im März einen Wettbewerb für Mathe-Comics ausgeschrieben, es wurden 39 BDs eingesandt, die auf images.math.cnrs.fr/Concours-BD-a-vous-de-voter.html ausgestellt sind und für die noch bis zum 20.8. abgestimmt werden kann.In den meisten Comics geht es um Schulmathematik, von...

Auch beim Copyright?Dieses Bild ist ein Selbstporträt: der abgebildete Makake hat es selbst aufgenommen, wie die Daily Mail am 5.7. berichtete.Und dieses Bild hat jetzt zu einem bizarren Copyright-Streit geführt: nachdem Tech Dirt das Foto am 7.7. für einen Artikel Monkey Business: Can A Monkey License Its Copyrights...

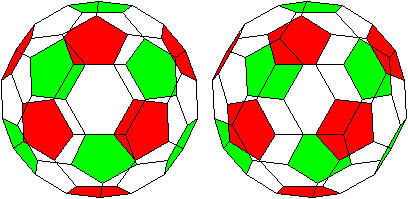
Aufgeweichte Nüsse knacken (wieder mal): Eulers Polyederformel beweisen mit Homologiegruppen.Letzte Woche hatten wir angefangen über die Eulersche Polyederformel und ihre Verallgemeinerung (für beliebige Flächen) zu schreiben.Worum ging es bei der Eulerschen Polyederformel?Wir zerlegen eine Fläche in Polygone und...