Das hat jetzt mal nichts mit Mathematik zu tun, aber vielleicht interessiert es ja einige der (laut Google Analytics recht zahlreichen) Berliner Leser dieses Blogs, daß ein auf Berlins Dächern und in Berlins U-Bahnen spielender Film momentan eines der Hauptthemen auf den Kulturseiten koreanischer Zeitungen ist.Eine...

von Thilo KüssnerWir hatten im letzten Jahr häufig über den Elsevier-Boykott berichtet, bei dem es vor allem gegen die viel zu hohen Preise von Fachzeitschriften in kommerziellen Verlagen ging. (Zuletzt hier.) Inzwischen gibt es im mathematischen Publikationswesen neue Entwicklungen, über die man sicher geteilter...

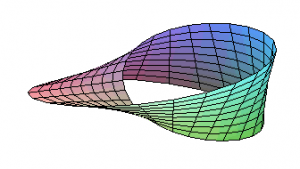
Charakteristische Klassen sollen messen wie getwistet (verdreht) ein Bündel ist. Das Möbiusband zum Beispiel ist - als Bündel über dem Mittelkreis betrachtet - verdrehter als ein Kreisring:weshalb seine charakteristischen Klassen komplizierter sein sollten. (Der Kreisring ist - als Bündel...

Der Boykottaufruf gegen Elsevier ist jetzt gut ein Jahr alt, mit 13195 Unterzeichnern, davon 2237 Mathematiker.Es ging damals in erster Linie um die völlig überhöhten Preise der bei Elsevier verlegten Fachzeitschriften.Es hatte dann im Mai einen offenen Brief Elseviers mit verschiedenen...

Es gehört seit Jahrzehnten zu den mittelgroßen offenen Problemen der Mathematik: der Komplexitätsstatus des Graphenisomorphie-Problems. Worum geht es? Einen Graphen kann man sich vorstellen wie eine Straßenkarte, wobei die Straßen im Allgemeinen auch mit Über- und Unterführungen aneinander vorbei geführt werden...