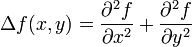Quantum Unique Ergodicity.Eine weitere Anwendung von hyperbolischer Geometrie und Modulformen ist "Quantum Unique Ergodicity" ("Quanten-eindeutige Ergodizität" ist wohl die passendste Übersetzung?)Bei "Quantum Unique Ergodicity" geht es um "Wellen mit hohen Frequenzen", also Eigenfunktionen des Laplace-Operators zu...

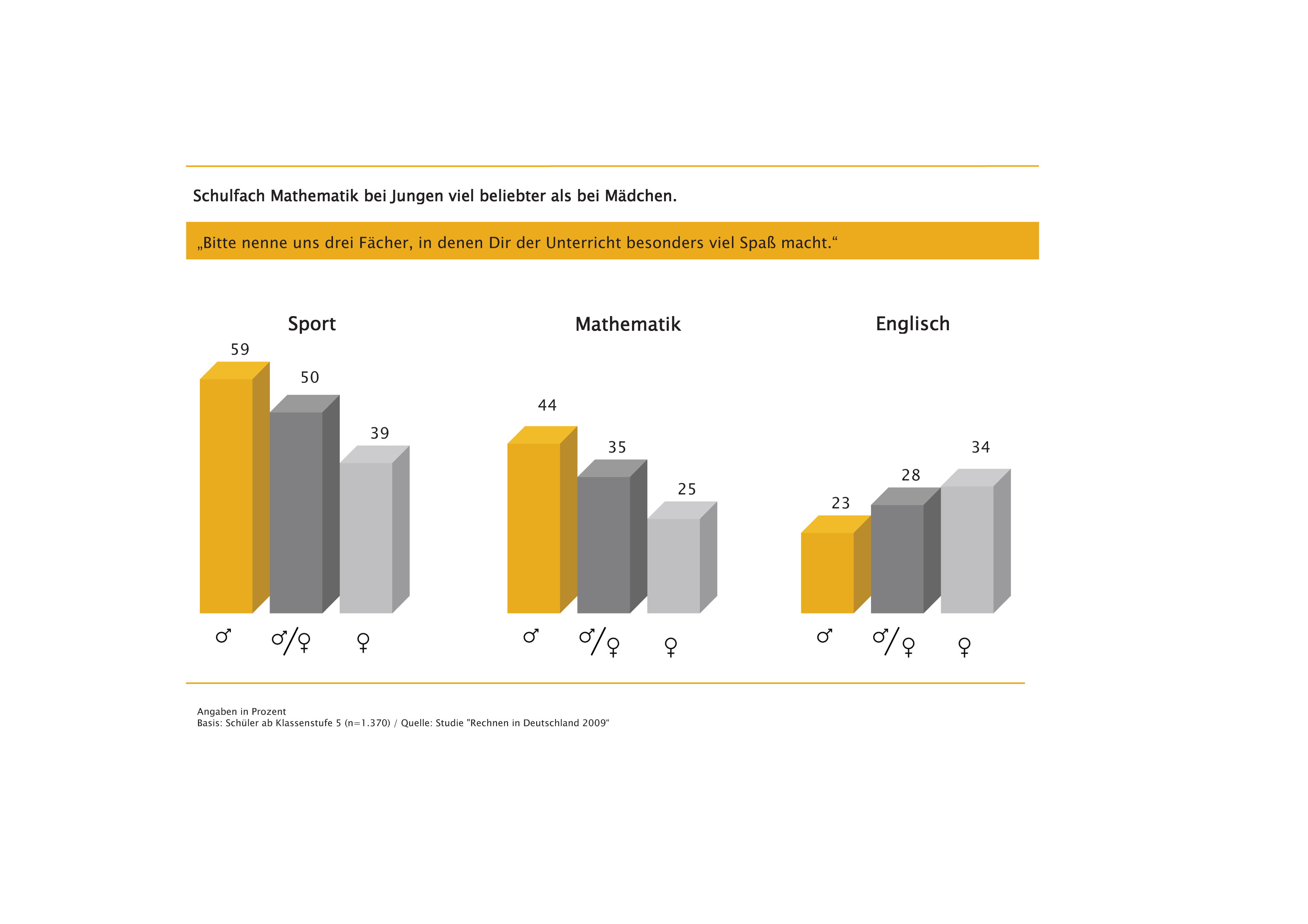
Eine neue forsa-Studie zeigt, was wir schon immer wußten: die Mehrheit der 18-65-jährigen gibt Mathe als ihr Lieblings-Schulfach an. Auf den nächsten Plätzen folgen Sport, Geschichte und Geographie. Die SZ kommentiert die Studie mit der Überschrift "Was sich haßt, das liebt sich". Und das Hamburger Abendblatt titelt...

"Keine Ahnung von Mathematik zu haben ist nicht cool" hieß neulich ein Artikel auf den scienceblogs. Diese Erfahrung haben jetzt auch 93 Lehrer einer High School in Rhode Islands gemacht.Wie n-tv gerade unter der Überschrift "Schlechte Mathe-Note Alle Lehrer an US-Schule gefeuert" meldet, hat die Schulbehörde alle 93...

In der Bevölkerung genießt das Schulfach Mathematik große Popularität. Viele Erwachsene haben ihren Mathematikunterricht auch nach Beendigung der Schulzeit in guter Erinnerung. Das Fach belegt bei den Befragten zwischen 18 und 65 Jahren Rang eins (40 Prozent) der populärsten Schulfächer und ist somit das Lieblingsfach...

Noch einige Erklärungen zum mathematischen Hintergrund von SnapPy:SnapPy 1.1 hatten wir im vorigen Artikel vorgestellt. Hier noch eine kurze Beschreibung, worum es aus mathematischer Sicht eigentlich geht.Konstruktion 3-dimensionaler MannigfaltigkeitenJede 3-dimensionale Mannigfaltigkeit kann konstruiert werden durch...