Die Neural Correlate Society veranstaltet seit 2004 jährlich den Wettbewerb 'Best Visual Illusion of the Year'.Platz 1 geht dieses Jahr an The break of the curveball (Arthur Shapiro, Zhong-Lin Lu, Emily Knight, & Robert Ennis, University of Southern California) - die Animation eines senkrechten fallenden Balles...
Ein Gericht hat die Praxis eines kalifornischen Schulbezirks gestoppt, Dopingtests für Teilnehmer an Musik-Wettbewerben, Mathematik-Olympiaden oder gar Schweinezucht-Wettbewerben1 vorzuschreiben.Die Tests waren letztes Jahr eingeführt worden, dagegen geklagt hatte die American Civil Liberties Union of Northern...
"Traders to Teachers" - New Jersey schult arbeitslose Banker in Schnellkursen zu Mathe-Lehrern.Die NYT berichtet über das neue Projekt "Traders to Teachers", in dem arbeitslose Finanzberater zu Mathe-Lehrern umgeschult werden.Die Teilnehmer (die meisten wohl zwischen 40 und 50 und mit Uni-Abschlüssen in 'finance' oder...
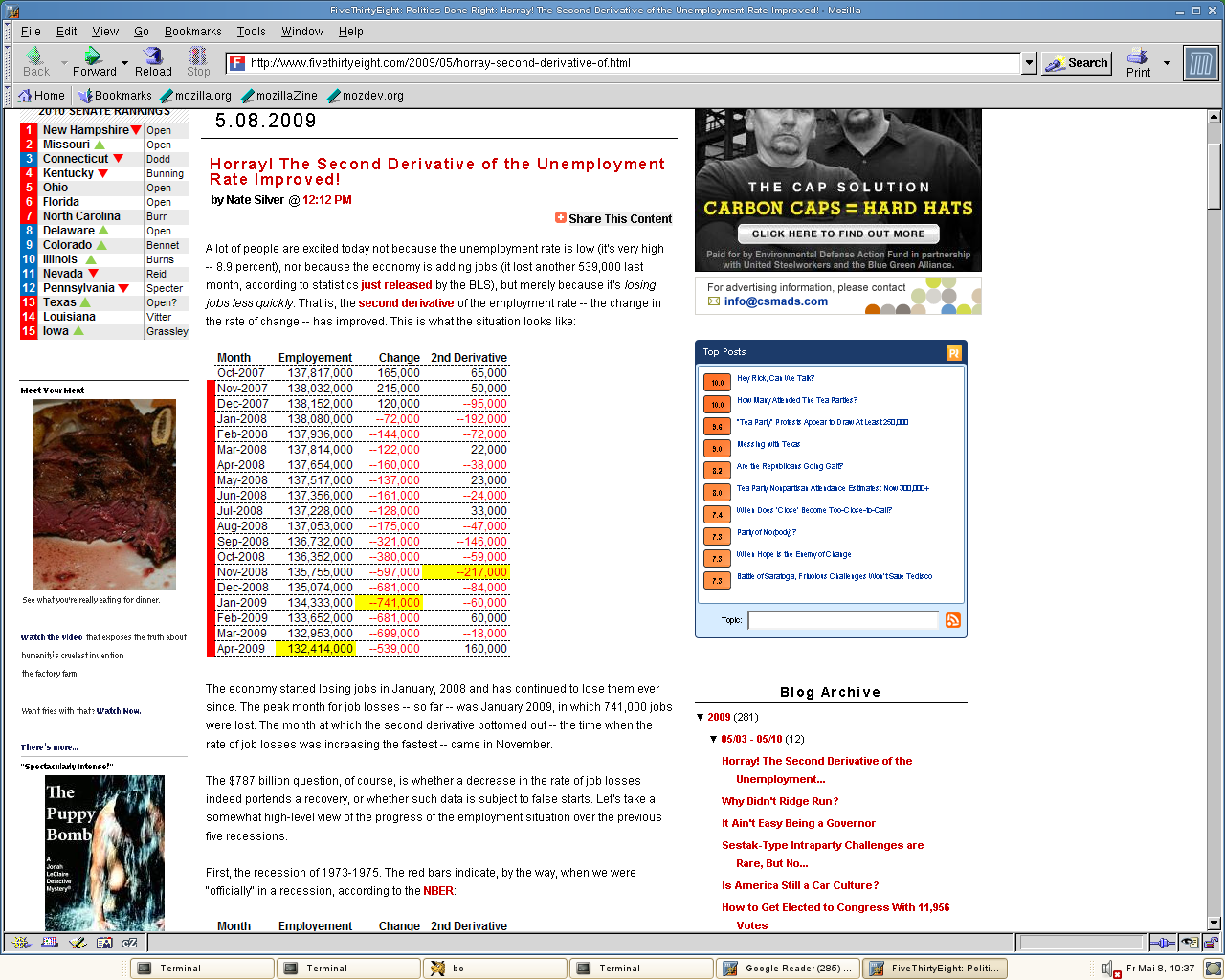
"Ökonomen sehen Ende des Abschwungs" titelt heute Spiegel online... und auch aus den USA kommen gute Nachrichten: die 2.Ableitung der Beschäftigtenzahl hat zugenommen, deren 3.Ableitung ist also positiv.Im Klartext: die Arbeitslosenzahl hat zugenommen, auch der monatliche Zuwachs an Arbeitslosen (die 1.Ableitung) hat...
Überlagerungen der Brezelfläche und Symmetrien der hyperbolischen Ebene.Der Nutzen der Überlagerungstheorie besteht darin, daß es zu jeder Fläche eine einfach zusammenhängende Überlagerungs-Fläche gibt und daß man damit Fragen über Flächen auf Fragen über Symmetrien einfach zusammenhängender Flächen zurückführen...